Porque devemos ter cuidado ao usar o PSM (Propensed Score Matching)
Porque devemos ter cuidado ao usar o PSM (Propensed Score Matching)
Nesse breve texto gostaria de refletir sobre um tema recorrente dentro das ciências econômicas, mais especificamente dentro da análise de politicas públicas, e suas discussões metodológicas que é sobre a aplicação do PSM em estudos sobre analise de impactos.
Motivação
Assim como muitos trabalhos também acabei usando a metodologia PSM em minha monografia da graduação, de inicio achava que seria o suficiente para um trabalho de nível inicial, mas ao buscar a literatura metodológica acabei percebendo que o buraco era mais embaixo, sendo o ponto de partida de King & Nielsen (2018), e mesmo para um trabalho mais simples, seria interessante agregar mais metodologias que garantissem uma maior robustez do trabalho.
Vocês podem encontrar a monografia que inspirou e um artigo derivado dela aqui, ou direto no meu github.
O que é o PSM ?
O ponto de partida para a aplicação do PSM se da na estimação do que chamamos de ATT (Average Treatment on Treated), ou seja efeito médio do tratamento no tratados.
O ATT é uma das principais metodologias de avaliação de impacto utilziadas na literatura de ciências sociais aplicadas, e principalmente dentro da avaliação de políticas publicas, a estimação consiste em estimar a diferença de uma variável alvo, entre observações expostas/tratadas a um evento, quando comparadas a observações não expostas/tratadas a esse mesmo evento, o ATT pode ser representado pela formula abaixo:
\[ATT = E(y_{i} | D = 1) - E(y_{i} | D = 0)\]O grande problema dessa metodologia quando pensada em ciências sociais, é que não podemos replicar os resultados para individuos em duas realidades ou oportunidades, portanto não conseguimos estimar um ATT que seja puro e demonstre de forma totalmente pura o efeito do tratamento, dessa forma dada a aplicação de uma política, ou de um evento que afeta parte de uma população devemos encontrar outros meios de estimar o efeito dos tratados, é ai que entra a aplicação do PSM e outros procedimentos de Matching.
Dentro desse contexto em que não conseguimos replicar um individuo em duas situações diferentes o que podemos fazer no caso é comparar as duas populações, porém ao invés de aplicarmos de forma direta, selecionamos as observações do grupo controle que tenham um conjunto de características observaveis o mais parecida com cada observação do grupo controle, sendo assim ai que entram as técnicas de matching.
O PSM surge como uma proposta para “driblar” o problema do ATT sugerido por Rubin (1983), em essencial o Propensed Score seria a probabilidade condicional de se participar de um tratamento dado um conjunto de variáveis observáveis. A primeira premissa do PSM é que os resultados potências $Y_{0}$ sendo apenas baseadas em características observáveis;
\[Y_{0}, Y_{1} \perp D|X\]A segunda condição é que para cada observação tratada, existe um par controle que reproduziria o resultado do indíviduo tratado na ausência de tratamento, essa hipótese é representada por:
\[0 < P(D=1|X) < 1\]1. Criação do Propensed Score
A primeira é a que busca criar um score de propensão baseada na amostra de tratados em que características observaveis são utilizadas para a construção desse score, que significaria : Dada as características observaveis dessa observação qual seria a probabilidade dessa ser uma observação tratada. Os calculos são efetuados por meio da aplicação de uma regressão logística como segue exemplo abaixo:
\[\pi = \frac{exp( -\beta 'X )}{1+exp( -\beta 'X )}\]2. Calculo das distâncias
A partir da estimação do Propensed Score para a amostra como um todo agora devemos calcular as distâncias entre os scores das observações tratadas e as controles, a partir desse calculo podemos selecionar as observações que mais se aproximam em relação ao score.
\[d = | \hat{ \pi_{c} } - \hat{\pi_{t}} |\]3. Seleção dos k mais próximos
A partir das distâncias calculadas selecionamos as k observações mais próximas de cada observação tratada e a partir dai temos o matching completo, assim poderiamos estimar um ATT dada a diferenciação entre grupos e portanto teriamos amostras conntrole e tratadas com uma série de características observaveis semelhantes e portanto nosso ATT estimado incorreria em menor erro.
\[min_k( d( \hat{ \pi_{c} }, \hat{\pi_{t}} ) )\]Resumo
O PSM como demonstrado de fomra simplória acima, funciona como uma redução de dimensões de um procedimento clássico de Matching como o KNN ( K Nearest Neighbours ), porém ao invés de realizar o procedimento sobre o vetor de variáveis observadas, realizamos sobre o score de propenção, um ponto posítivo sobre a realização dessa técnica é que diante condições em que possuimos muitas caracteristicas observaveis, a aplicação de um KNN sobre todas elas implicaria em um auto tempo de processamento, assim o PSM reduz o número de dimensões de n para apenas uma.
Porém ao mesmo tempo a redução de dimensões pode apresentar um lado negativo que é o fato do matching sofrer problemas e não conseguirmos parearmos observações do grupo controle que sejam pareadas as tratadas que realmente tenham características similares, e portanto podemos ter erros em não selecionarmos as observaçoes que são mais próximas.
Exemplos Práticos
set.seed( 1200 )
data <-
data.frame(
x1 = c( rnorm( 500, mean = 10, sd = 25 ),
rnorm( 120, mean = 23, sd = 20 ) ) ,
x2 = c( rnorm( 500, mean = 34, sd = 17 ),
rnorm( 120, mean = 53, sd = 19 ) ) ,
y = c( rep(0, 500), rep(1, 120 ))
)Estatísticas descritivas básicas das variáveis :
| Estatística | $Y$ | $X_{1}$ | $X_{2}$ |
|---|---|---|---|
| Min | 0 | -65.930 | -14.23 |
| 1st Qu. | 0 | -2.356 | 24.93 |
| Median | 0 | 14.171 | 36.34 |
| Mean | 0.1935 | 13.015 | 37.70 |
| 3rd Qu. | 0 | 28.877 | 49.45 |
| Max | 1 | 92.046 | 99.26 |
Descrição das estatísticas básicas por Tratamento/Controle:
| Tratamento | Estatística | $X_{1}$ | $X_{2}$ |
|---|---|---|---|
| Min | -27.252974 | 13.93817 | |
| 1st Qu. | 12.529418 | 38.48299 | |
| Sim | Median | 22.634250 | 52.04538 |
| Mean | 23.222553 | 53.57092 | |
| 3rd Qu. | 36.437639 | 69.29709 | |
| Max | 67.587539 | 99.26132 | |
| Min | -65.930316 | -14.22998 | |
| 1st Qu. | -6.815461 | 22.98394 | |
| Não | Median | 10.579938 | 33.57835 |
| Mean | 10.565734 | 33.88806 | |
| 3rd Qu. | 27.718731 | 45.07952 | |
| Max | 92.046170 | 84.87077 |
Resultado da Regressão Logística :
Call:
glm(formula = y ~ x1 + x2, family = "binomial", data = data)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.8061 -0.5848 -0.3926 -0.2085 2.4764
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -4.390128 0.356175 -12.326 < 2e-16 ***
x1 0.023382 0.005062 4.620 3.84e-06 ***
x2 0.058949 0.006590 8.946 < 2e-16 ***
---
Signif. codes: 0 ’***’ 0.001 ’**’ 0.01 ’*’ 0.05 ’.’ 0.1 ’ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 609.25 on 619 degrees of freedom
Residual deviance: 481.30 on 617 degrees of freedom
AIC: 487.3
Number of Fisher Scoring iterations: 5Observação do Matching:
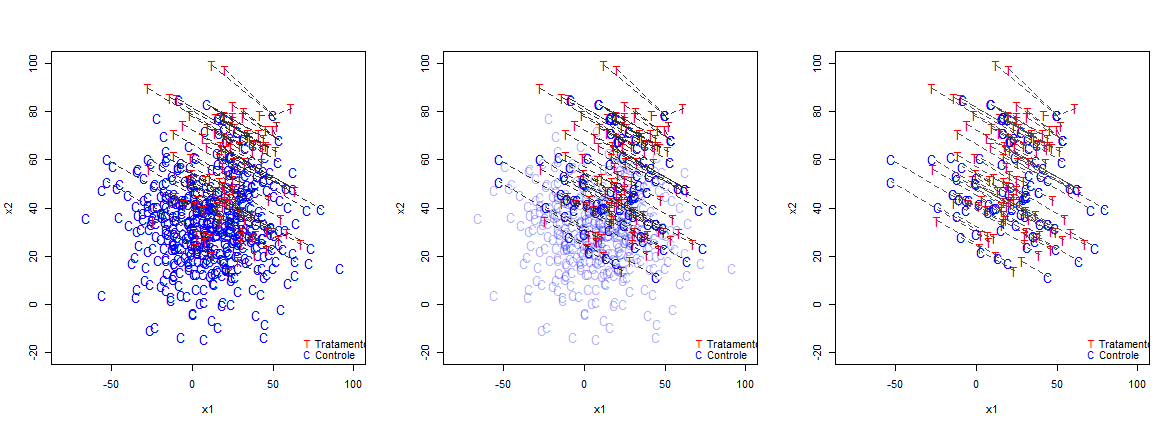
Olhando os plots bi-dimencionais abaixo podemos perceber como se dá o pareamento pelo PSM e a distância das caracteristicas observaveis $X_{1}$ e $X_{2}$ dos dois grupos em um plot.
 </a>
</a>
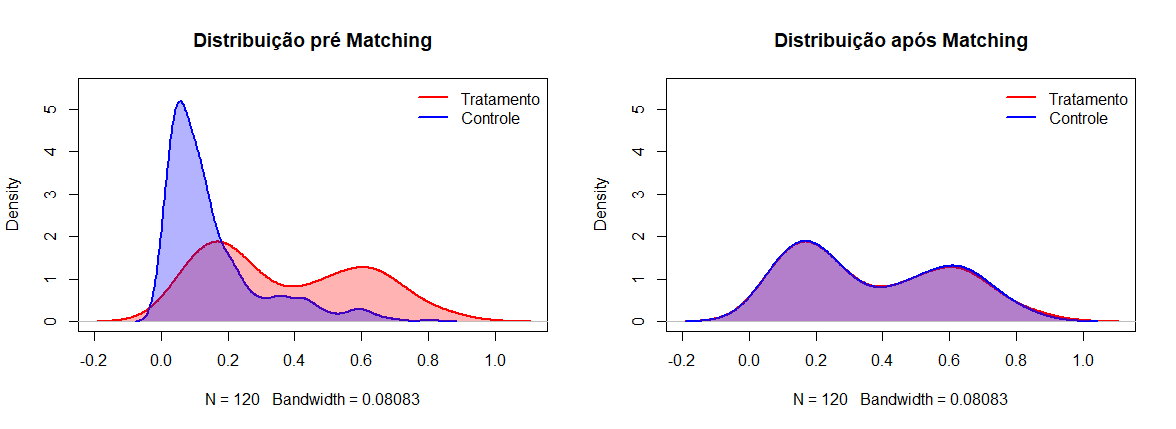
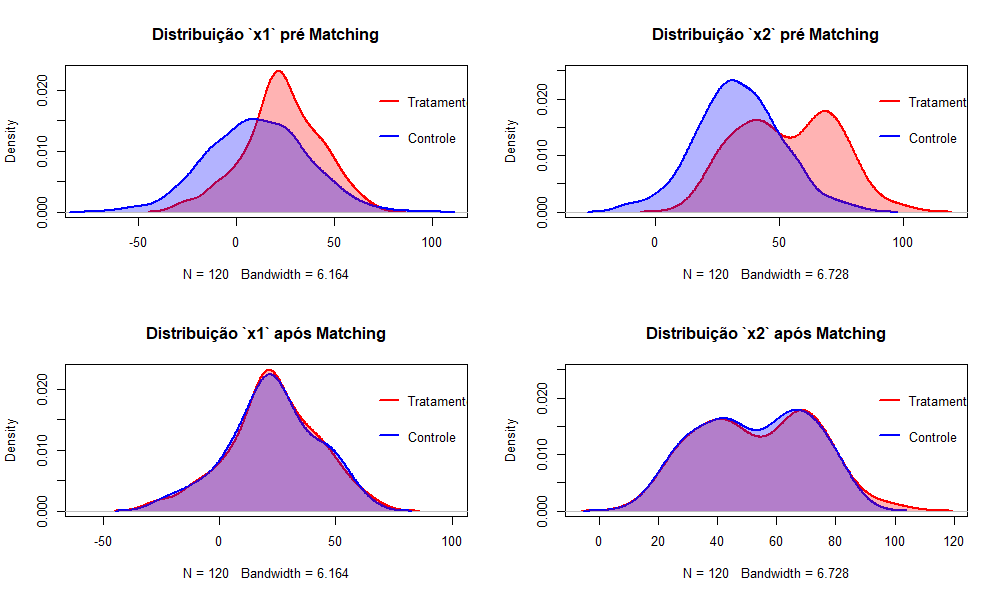
Olhando o passo a passo vemos que as observações pareadas não são necessariamente os mais próximos e de certa forma parece existir um certo padrão de seleção, aonde observaçoes de um certo angulo são selecionadas, a baix vemos as densidades dos Scores e das variáveis $X_{1}$ e $X_{2}$ antes e depois do pareamento do PSM
 </a>
</a>
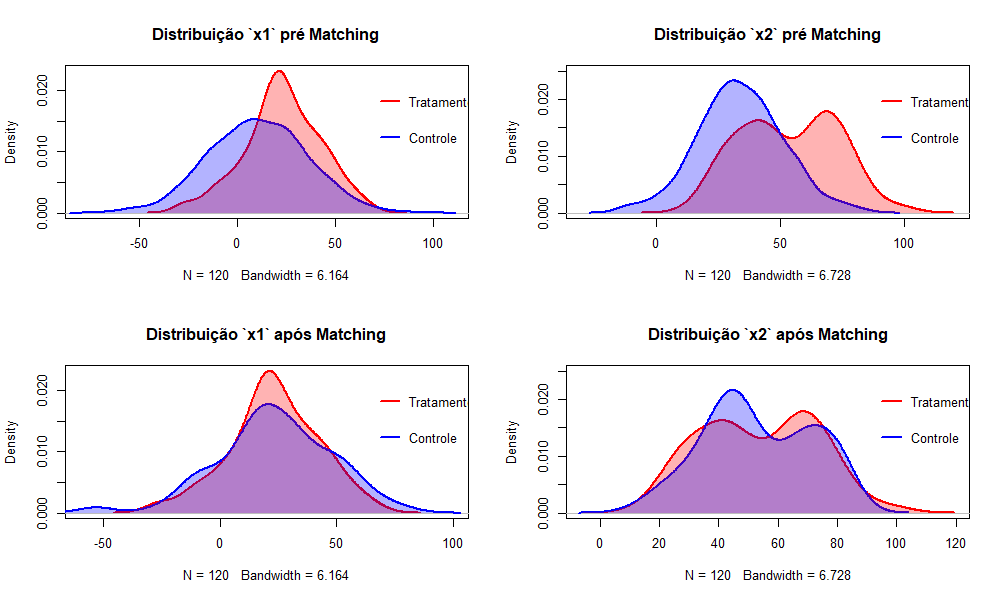
Como podemos ver, a distribuição dos scores acaba se aproximando muito, mostrando um gráfico em que há sobreposição quase que exata das curvas, porém quando olhamos a nível da variável não necessariamento isso se traduz, havendo algumas diferenças entre as distribuições.
 </a>
</a>
Metodologias complementares
A questão toda envolvendo o PSM, não é que não devemos utiliza-lo, mas sim que sua utilização precisa de um maior cuidado, e que metodologias alternativas devem ser usadas como forma de validação e comparação dos resultados.
Distância de Mahalanobis
Como mostrado em King & Nielsen (2018), uma metodologia capaz de demonstrar matchings robustos é a distância de Mahalanobis.
A distância é definida pela formula abaixo, aonde $\vec{x}$ e $\vec{y}$ são vetores de características observaveis das observações tratadas e controle, e $S^{-1}$ é inversa da matriz de correlação das características observaveis.
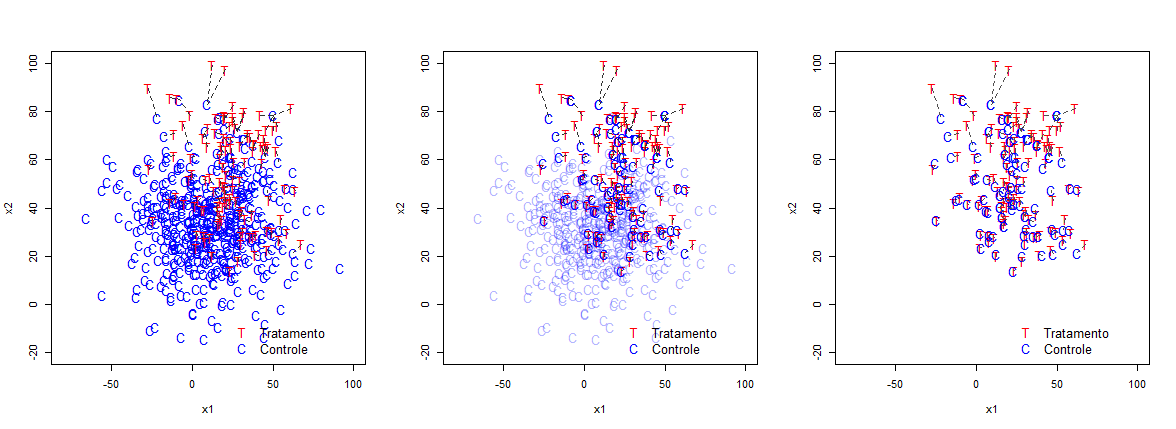
\[d(\vec{x} , \vec{y}) = \sqrt{( \vec{x} - \vec{y} )S^{-1}( \vec{x} - \vec{y} )}\]Essencialmente se trata de uma distância euclidiana ponderada pela matriz de correlação das variaveis. A grande vantagem que veremos abaixo é o fato de realmente parearmos sempre os pontos com caracteristicas mais próximas, evitando problemas de incorrência do erro de selecionarmos individuos que tenham características diferentes, porém a contrapartida é que se trata de um processo e matching bem mais intensivo computacionalmente.
 </a>
</a>
 </a>
</a>